Существует множество способов расчета вероятности событий в футбольных матчах, но один из самых простых методов основан на базовой статистике. Для расчета вероятности достаточно знать результаты последних 10 матчей команд.
Вероятность счёта серии матчей в бернуллиевской модели
Недавно, наблюдая за неформальным онлайн-турниром по соревновательной игре, я наткнулся на следующее утверждение: если в игре с двумя победителями участвуют две равные команды, т.е. если исход игры определяется симметричным броском монеты, то вероятность одностороннего исхода, т.е. 2-0/0-2, равна вероятности неравностороннего исхода, т.е. 2-1/1-2. Это утверждение заставило меня извлечь из глубин памяти школьные знания по комбинаторике и теории теорем. Позвольте мне дать краткую справку по этой теме.
Две команды, команда 0 и команда 1, играют в серию игр. Исходы различных игр в серии являются независимыми случайными величинами со следующим распределением. Вероятность того, что команда 0 выиграет игру, равна, вероятность того, что команда 1 выиграет игру, равна. Предположим, что, т.е. ничьей быть не может.
Игры в серии проводятся до тех пор, пока одна команда не выиграет серию. Формат «first to» (FT ) эквивалентен формату «best of» (BO ), где победитель определяется серией игр определенной продолжительности — если команда уже выиграла, ее соперник не может выиграть снова, т.е. она не может победить.
Законченную серию игр можно представить в виде последовательности нулей и единиц, где в позиции номер означает, что игру выиграла команда 0, а в позиции номер означает, что игру выиграла команда 1. Пример такой последовательности:
В этом примере команда 0 выиграла 4:2 в FT4/BO7. В дальнейшем для обозначения результата мы также будем использовать обозначение следующего вида:, указывая количество побед команды 0 и количество побед команды 1. Это означает, что приведенная выше оценка может быть записана следующим образом: Каждый счет завершенной серии игр может быть представлен следующим образом: в случае победы команды 0 и в случае победы команды 1. Обратите внимание, что команда-победитель серии игр обязана выиграть последнюю игру серии, т.е. в случае победы команды 0 серия должна закончиться со счетом, а в случае победы команды 1 серия должна закончиться со счетом. Количество нулей в серии — это количество побед команды
Вероятность определённого счёта в серии матчей
Серия матчей между двумя командами, где в каждом матче исход (победа команды 0 или победа команды 1) является случайной величиной с указанными выше вероятностями, может быть смоделирована как последовательность случайных величин, подчиняющихся распределению Бернулли. Если исходы отдельных пар независимы, то вероятность того, что в результате получится последовательность, равна произведению вероятностей отдельных элементов. Например, для последовательности, описанной выше, вероятность такой серии совпадений составляет. Однако один и тот же счет может соответствовать разным сериям матчей. Например, оценка может быть получена из следующей последовательности:
Необходимо подсчитать общее количество возможных серий для любого балла.
Серия игр с таким результатом (т.е. с командой 0 в качестве победителя) содержит ровно нули. Поставьте единицы в последовательности нулей. Для первой единицы есть ровно столько позиций, куда можно вставить единицу (потому что последовательность должна заканчиваться нулем, а последовательность игр должна заканчиваться победой команды 0). Следующий блок вставляется в последовательность игр, т.е. существуют возможные позиции, в которые он может быть вставлен. Если предположить, что все вставленные единицы уникальны, это приводит к тому, что
Вариации вставки единиц в исходную последовательность нулей. Напомним, что любое преобразование единиц не изменяет результирующую последовательность. Это означает, что результат нужно разделить на количество перестановок единиц, что одно и то же. Результат
Общая вероятность подсчета составляет .
Для подсчета, вероятность также равна .
Проверка состояния нормализации
Результаты
Давайте сначала просто рассмотрим распределение с произвольно выбранными параметрами:
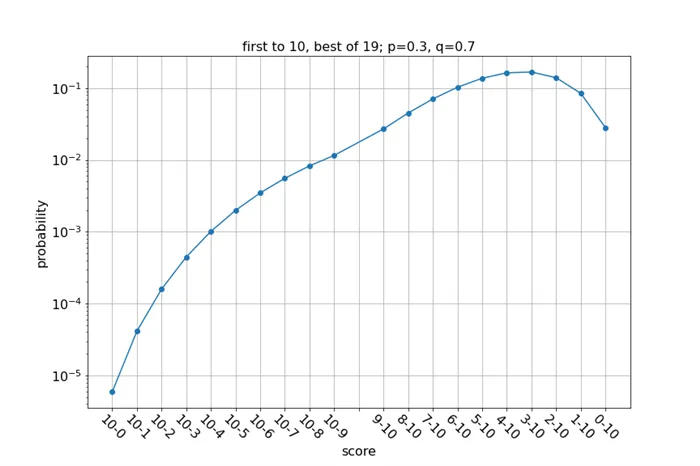
График асимметричен, поскольку максимальная вероятность приходится на графы 3-10, что согласуется с приведенными вероятностями. Как меняются кривые при изменении вероятности победы в игре?
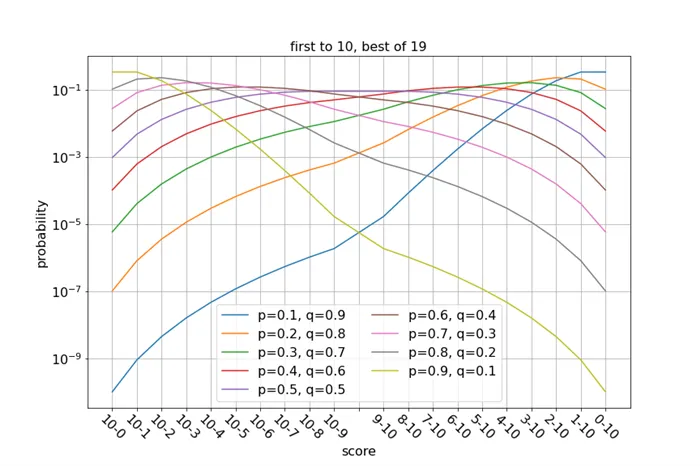
Некоторые значения, похоже, имеют одинаковую вероятность — например, вероятность для 0-10 и 1-10 не изменилась. Вернемся к формулам, выведенным ранее. Вероятность забить гол равна. Вероятность подсчета составляет. То есть, вероятности оказываются равными в. Хотя вероятность более длинной серии игр для счета меньше, чем вероятность более короткой серии игр для счета, вероятность счета равна вероятности. из-за увеличения числа серий, в которых достигается счет.
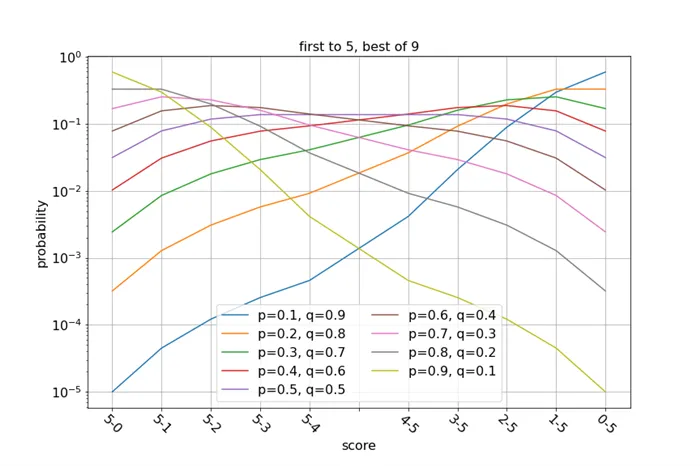
Это объясняется тем, что такой исход уже наблюдается для и, в то время как для и вероятность является монотонной функцией оценки. Замечание о том, что вероятность является монотонной функцией оценки для каждого случая, в котором либо, оставим на усмотрение читателя.
Мы также наблюдаем равенство вероятностей для оценок 10-8, 10-9, 9-10, 8-10 и для оценок 3-5, 4-5, 5-4, 5-3. Мы хотим показать, что для каждого при вероятность подсчета равна вероятности подсчета.
Вероятность подсчета в этом случае равна, а вероятность подсчета равна .
Полученный результат легко объясняется моделью: Для счета и для счета в серии игр необходимо определить счет после данной игры. Из последнего результата может получиться только один результат или один результат с равной вероятностью.
Так, для формы FT2/BO3, если команды равны и исход матча определяется симметричной монетой Бернулли, вероятности исходов 2-0/0-2 и 2-1/1-2 одинаковы и равны соответственно. Однако означает ли это, что конечный результат формата FT2/BO3 не дает никакой информации о силе и вероятности команд-победителей?
Обратите внимание, что формулы, полученные нами ранее для вероятностей попадания, позволяют нам найти ML-оценки для вероятностей выигрыша и. Вероятность попадания пропорциональна произведению. Логарифм вероятности равен. для постоянной суммы. Если мы продифференцируем логарифм вероятности по и установим производную равной нулю, то получим условие экстремального значения: .
Это дает оценки для вероятностей : ,. Доказательство того, что эти оценки максимизация логарифм вероятности, мы оставляем на усмотрение читателя.
Таким образом, хотя формат FT2/BO3 недостаточен для точной оценки относительной силы ордеров, некоторую информацию можно извлечь из ML-подхода. Рассмотрим, как меняется функция правдоподобия для фиксированной оценки:
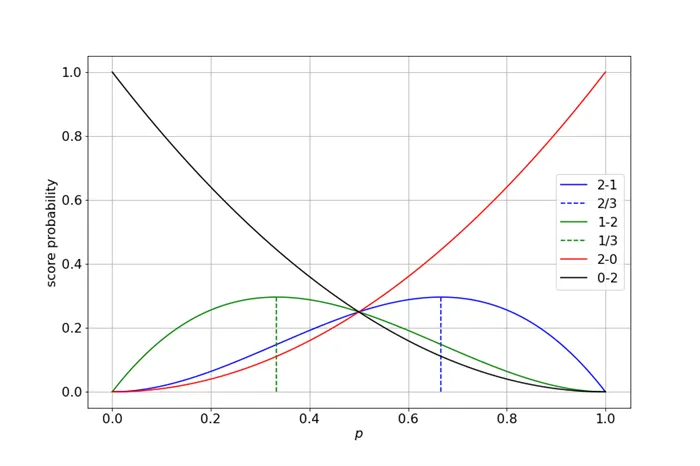
Вероятности для исходов 2-0 и 0-2 берут максимальное количество очков, соответствующее однозначной победе соответствующей команды. Вероятности для 2-1 и 1-2 принимают максимальное значение по очкам и соответственно, т.е. результат с победой проигравшей команды сильнее указывает на ничью, чем результат с одним голом. Как зависит вероятность игры в один гол в FT2/BO3?
График асимметричен, поскольку максимальная вероятность приходится на графы 3-10, что согласуется с приведенными вероятностями. Как меняются кривые при изменении вероятности победы в игре?
Кто такой военнообязанный?
Учету подлежат не только военнослужащие, находящиеся на службе, но и контрактники. В число призывников входят гражданские лица
- Резервисты: лица, завершившие военную службу, и лица, уволенные со службы в резерве,
- выпускники военных вузов (военных учебных центров) или выпускники военной кафедры
- не прошли военную службу по причине освобождения от военной службы (например, низший класс здоровья «В»)
- Отказался от призыва в армию из-за отсрочки по достижении 27-летнего возраста.
- Не прошел службу без причины в возрасте 27 лет или завершил гражданскую службу.
- Призывники в возрасте от 18 до 27 лет, не находящиеся в резерве, не подлежат обязательной военной службе, но могут быть призваны на военную службу.
Кого должны призвать по частичной мобилизации?
- Обязательная военная служба,
- Лица, имеющие боевой опыт
- Офицеры и унтер-офицеры в возрасте до 35 лет
- Унтер-офицеры в возрасте до 50 лет
- Государственные служащие в возрасте до 55 лет
- Гражданские лица некоторых военных профессий, особенно стрелки, экипажи танков, артиллеристы и водители
- работники предприятий оборонной промышленности
- аккредитованные ИТ-компании,
- финансовые учреждения,
- коммуникации,
- СМИ
- исключить из списка системно значимых компаний,
- Лица, которые временно не имеют права на участие в программе по состоянию здоровья,
- лица, ухаживающие за членом семьи или человеком с инвалидностью I группы,
- Работники, имеющие четырех или более детей в возрасте до 16 лет, и матери которых имеют четырех или более детей в возрасте до 8 лет и воспитывают их без супруга или супруги
- Военные пенсионеры, независимо от принадлежности к вооруженным силам, вышедшие на пенсию (старше 65 лет или по состоянию здоровья) и снятые с воинского учета.
- Лица, постоянно проживающие за пределами России и не состоящие на учете в вооруженных силах.
* Однако могут быть призваны лица, отсутствующие непродолжительное время и состоящие на воинском учете по месту жительства в России.
Какие есть категории запаса?
Категория военнослужащих указывается на странице 11 военно-учетной карточки. Там же можно посмотреть информацию о регистрационной группе и составе, узнать воинскую должность и предмет регистрации.

На странице 11 указан специальный военный регистрационный номер. Это специальность, которую человек получает во время службы в армии. Неважно, является ли этот человек инженером или руководителем. Когда его снова призовут на службу, он может стать, например, оператором радара или радистом.
Существует пять основных категорий:
- Категория «А» — подходит для военной службы,
- Категория «А» — класс А. Категория А — категория А. Категория В — пригоден к военной службе с незначительными ограничениями,
- Категория «С» — ограниченная,
- Категория «D» — временно не годен к военной службе,
- Категория «D» — совсем не подходит.
Внутри основных групп существуют подкатегории.
На этапе мобилизации набираются лица категорий A, B, C и D. Если у человека со временем появляются проблемы со здоровьем или его возраст превышает пределы призыва, гражданин исключается из резервного списка.